-
Hosaya Polynomial and Weiner Index of Abid-Waheed Graph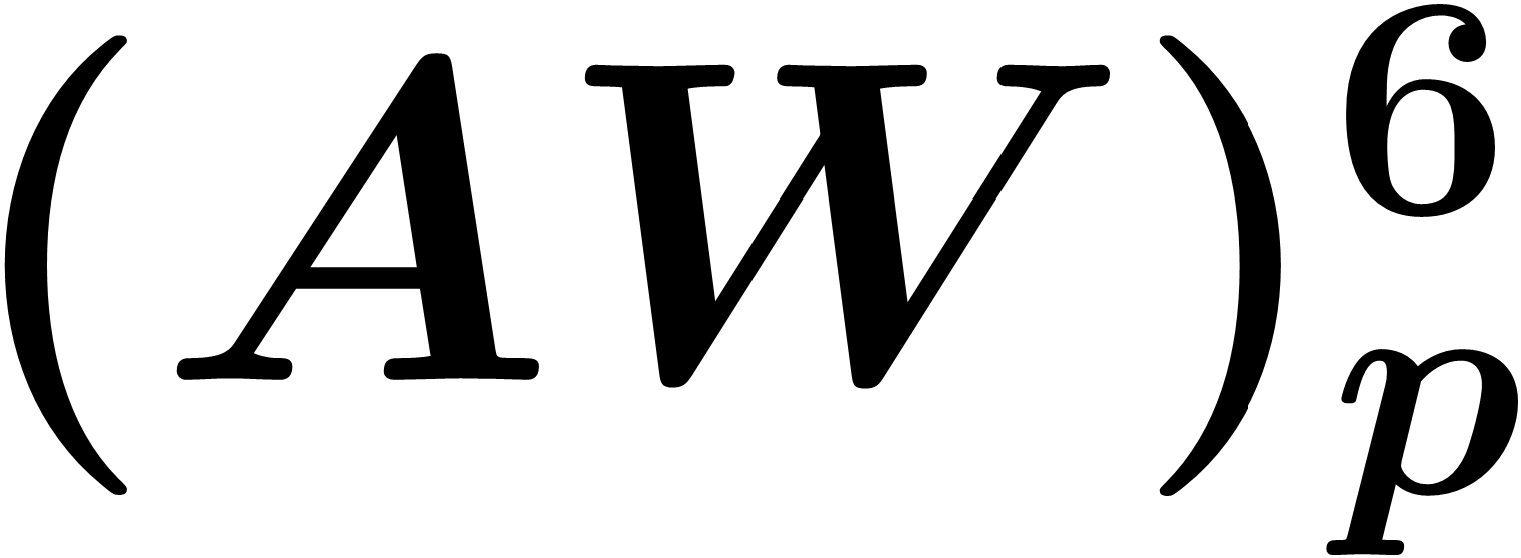 
Abid Mahboob,
Muhammad Waheed Rasheed
Issue:
Volume 11, Issue 4, August 2022
Pages:
89-94
Received:
17 August 2022
Accepted:
14 September 2022
Published:
27 September 2022
DOI:
10.11648/j.ijebo.20221003.13
Downloads:
Views:
Abstract: Graph theory is an area of mathematics and computer science that deals with graphs, or diagrams containing points and lines that represent mathematical truths pictorially. It has a broad scope of applications. The use of graph theory has exponentially increased. It is effective to understand the flow of computation, networks of communication, data organization, and Google maps in computers. Graphs have great importance in electrical engineering (design of electrical connections), linguistics (parsing of language trees, grammar of a language tree, phonology, and morphology), chemistry, physics, mathematics, and biology. Graph theory plays an important role in the development of theoretical chemistry. A special type of graph invariant called a topological index is a real number associated with the structure of a connected graph. In this paper, we calculate the Wiener index (WI) and Hosoya polynomial of newly defined “Abid Waheed graph ”.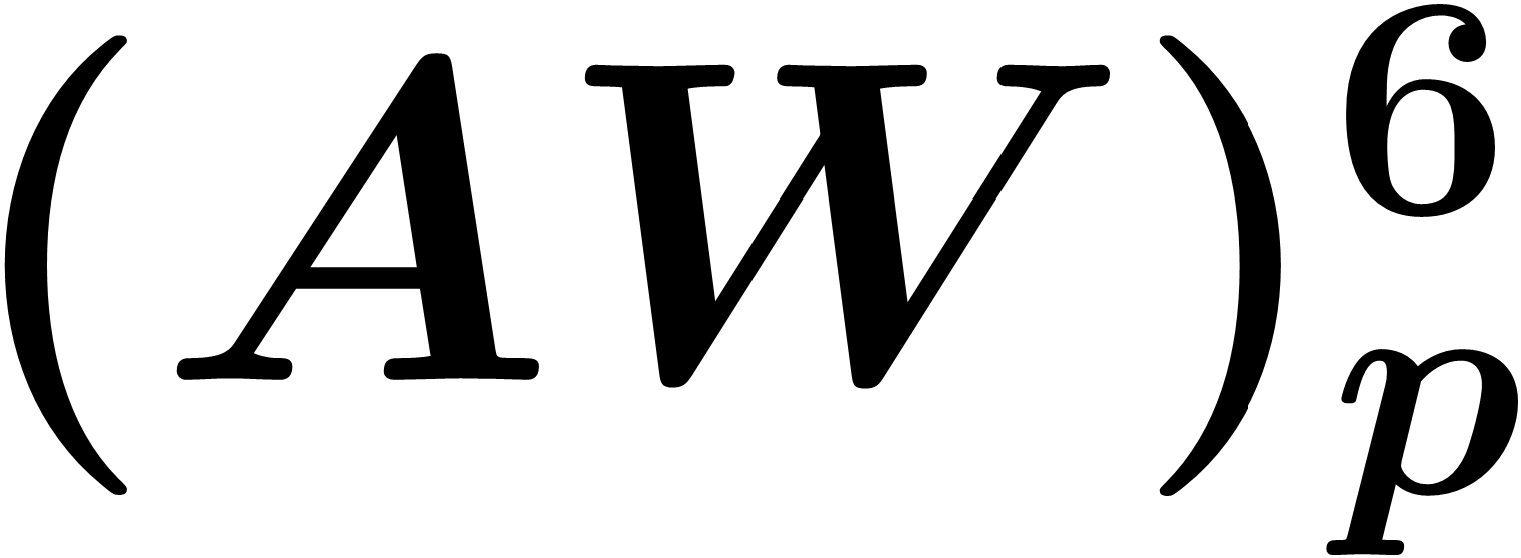
Abstract: Graph theory is an area of mathematics and computer science that deals with graphs, or diagrams containing points and lines that represent mathematical truths pictorially. It has a broad scope of applications. The use of graph theory has exponentially increased. It is effective to understand the flow of computation, networks of communication, data ...
Show More
-
Combination of Reduced Differential Transformation Method and Picard’s Principle
Yanick Alain Servais Wellot,
Gires Dimitri Nkaya
Issue:
Volume 11, Issue 4, August 2022
Pages:
87-94
Received:
30 June 2022
Accepted:
15 July 2022
Published:
22 July 2022
DOI:
10.11648/j.acm.20221104.11
Downloads:
Views:
Abstract: In this paper, the combination of methods is used for the search for exact solutions, when they exist of mixed and non-mixed nonlinear partial differential equations. it is the combinate of reduced differential transform method and Picard principle. This combination gave us an algorithm that promotes the rapid convergence of the problem given the exact solution desired. Some complex physical behaviors can be described by mathematical expressions. These expressions can be nonlinear partial differential equations and sometimes mixed. For a better understanding of the physical phenomena associated with such partial differential equations, the exact solution, when it exists, is better indicated. However, by using classical analytical methods, the access or the obtaining of the exact solution is not always obvious. With some hybrid algorithms, the difficulties of accessing this exact solution can be difficult or almost impossible. Hence the coupling of some algorithms to reach the desired result. The objective of our work is the search for exact solutions when they exist of mixed and unmixed nonlinear partial differential equations. Although the reduced transform method has presented several interesting results, the difficulties of obtaining exact solutions have also been encountered. Thus, in this paper, a combination is used to find exact solutions, when they exist, of these types of partial differential equations. It is the combination of the reduced transform method and Picard's principle. This Picard principle, which uses the Adomian decomposition method, works as a method of successive approximations, approaching the problem by an iterative scheme. This combination gave us an algorithm that favors the fast convergence of the problem. Thus, the exact solutions of the selected problems are obtained.
Abstract: In this paper, the combination of methods is used for the search for exact solutions, when they exist of mixed and non-mixed nonlinear partial differential equations. it is the combinate of reduced differential transform method and Picard principle. This combination gave us an algorithm that promotes the rapid convergence of the problem given the e...
Show More
-
The Modified Variational Iteration Method with Hermite Polynomials for the Numerical Solution of Tenth Order Boundary Value Problem
Otaide Ikechukwu Jackson,
Ishaq Ajimoti Adam,
John Obatarhe Emunefe,
Ayinde Muhammed Abdullahi
Issue:
Volume 11, Issue 4, August 2022
Pages:
95-101
Received:
1 July 2022
Accepted:
20 July 2022
Published:
17 August 2022
DOI:
10.11648/j.acm.20221104.12
Downloads:
Views:
Abstract: In this study, the numerical solution of tenth-order boundary value problems was obtained by employing the modified variational iteration method with Hermite polynomials. The correction functional is corrected for the boundary value problem (BVP) in this proposed method, and the Lagrange multiplier is optimally constructed using variational theory to reduce iteration on the integral operator while minimizing computational time. There was no need for any form of discretization or linearization with this method. The proposed modification also includes the generation of Hermite polynomials for the given boundary value problem and their use as the approximation's basis function. Four numerical examples were also provided to demonstrate the proposed method's effectiveness and reliability. Furthermore, we compared the results to some previously published findings. Tables 1, 2, and 3 show that our proposed method produces a better approximation to the exact solution than the Kasi Viswanadham & Sreenivasulu method, and Table 4 shows that our proposed method produces a better approximation to the exact solution in a few iterations than the Ali, Esra, Dumitru & Mustafa, and Iqbal et al. approaches, Rehman, Pervaiz, and Hakeem techniques (as can be seen from the tables of results). The calculations were carried out using the Maple 18 software.
Abstract: In this study, the numerical solution of tenth-order boundary value problems was obtained by employing the modified variational iteration method with Hermite polynomials. The correction functional is corrected for the boundary value problem (BVP) in this proposed method, and the Lagrange multiplier is optimally constructed using variational theory ...
Show More
-
Adaptive Type-II Hybrid Progressive Schemes Based on Maximum Product of Spacings for Parameter Estimation of Kumaraswamy Distribution
Issue:
Volume 11, Issue 4, August 2022
Pages:
102-115
Received:
7 June 2022
Accepted:
18 July 2022
Published:
17 August 2022
DOI:
10.11648/j.acm.20221104.13
Downloads:
Views:
Abstract: The present article aims to illustrate how the Adaptive Type-II Progressive Hybrid censoring scheme can be used to make statistical inferences regarding the shape parameters of the Kumaraswamy distribution. By adopting this scheme, one can reduce the total testing time and the cost associated with the failure of the units. Best of all, one can increase the effectiveness of the statistical analysis while reducing the total test time. The maximum product of spacings method (MPS) in classical estimation settings is highly effective. According to several authors, this method is a superior alternative to the maximum likelihood estimation method (MLE), which delivers more accurate estimates than the maximum likelihood estimation method. Our goal in this article is to estimate the shape parameters of the Kumaraswamy distribution by utilizing the MPS method. Asymptotic normality properties of the estimators are implemented to obtain approximate confidence intervals. In addition, bootstrap confidence intervals are calculated. Monte Carlo simulations have been carried out to compare the MPS and MLE methods. In order to assess the effectiveness of the proposed procedure, a numerical example based on real data is presented.
Abstract: The present article aims to illustrate how the Adaptive Type-II Progressive Hybrid censoring scheme can be used to make statistical inferences regarding the shape parameters of the Kumaraswamy distribution. By adopting this scheme, one can reduce the total testing time and the cost associated with the failure of the units. Best of all, one can incr...
Show More
